Những khái niệm cơ bản về thống kê mà hocthue.net tích lũy hơn 10 năm sẽ giúp ích bạn trong quá trình tra cứu, học tập về xác suất thống kê. Chúng tôi tổng hợp lại để giới thiệu, giúp bạn định hướng nghiên cứu về xác suất, thống kê thuận tiện hơn.
1. Biến và các chỉ số đánh giá mẫu.
Sự kiện ngẫu nhiên là gì? Trong cuộc sống có những sự kiện ngẫu nhiên, giả sử như số lượng người đi qua đường, sự kiện thiên thạch rơi vào trái đất, con bò nó đi vệ sinh vào thời điểm nào…. Gần như chúng ta không thể biết trước được những sự kiện như vậy và chúng ta gọi đó là sự kiện ngẫu nhiên.
Từ các sự kiện ngẫu nhiên khi dùng trong học thuật họ gọi là biến ngẫu nhiên. Biến (variable) được dùng trong khoa học khi chúng ta phải thống kê lại các sự kiện quy chúng về biến. Giả dụ người ta gọi X là biến số lượng thiên thạch rơi vào trái đất trong 10 năm tới.
Có 2 loại biến, biến ngẫu nhiên rời rạc và liên tục. Thông thường biến ngẫu nhiên rời rạc là các số nguyên như số lượng người ra vào một siêu thị (đếm được). Biến rời rạc thông thường là số thực, chẳng hạn như chiều cao của người dân Việt Nam.
Hàm mật độ xác suất nếu định nghĩa trong các sách sẽ là xác suất của biến ngẫu nhiên cho tất cả các giá trị của nó.
2. Các khái niệm cơ bản trong thống kê
Mỗi khái niệm ở trong thống kê có thể nói sẽ cần một bài viết dài về chính nó. Để hiểu về những khái niệm như vậy các bạn phải đọc các cuốn sách về thống kê để tìm hiểu rõ hơn.
Dưới góc độ tóm tắt hocthue.net giới thiệu 24 thuật ngữ thống kê gồm cả tiếng Anh để bạn tra cứu lại.
=
| Tiếng Việt | Tiếng Anh | Giải thích ý nghĩa bởi hocthue.net |
| Phân bố xác suất | Probability Distribution | Về mặt toán học, phân phối xác suất là hàm cung cấp xác suất của kết cục khác nhau trong một thử nghiệm. |
| Hồi quy | Regression | Mô hình quan hệ giữa biến độc lập và một hoặc nhiều biến độc lập |
| Kiểm định giả thuyết | Hypothesis Testing | Phương thức quyết định nếu có đủ chứng cứ bác bỏ giả thuyết khống về tổng thể. |
| Xu hướng trung tâm | Central Tendency | Đo lường trình diễn giá trị trung tâm hoặc tiêu biểu của bộ dữ liệu. Nói cách đơn giản |
| Thống kê bayer | Bayesian Statistics | Áp dụng xác suất để giải quyết vấn đề thống kê, cập nhật xác suất giả thuyết với chứng cứ mới. |
| Thống kê mô tả | Descriptive Statistics | Phương thức tóm tắt đặc điểm của bộ dữ liệu. |
| Phân bố (hoặc phân phối) | Distribution | Hàm (toán học) thể hiện độ phân tán của các điểm dữ liệu. |
| Lấy mẫu | Sampling | Lấy mẫu một bộ dữ liệu con (subset) từ tổng thể để ước lượng đặc tính của toàn bộ tổng thể. |
| Khoảng tin cậy | Confidence Interval | Một khoảng chứa tham số tổng thể, kế thừa từ thống kê mẫu. |
| Tương quan | Correlation | Đo lường mô tả 2 biến thay đổi cùng nhau, không giải thích đến nhân -quả. |
| Hiệp phương sai | Covariance | Đo lường quyết định hai biến khác nhau như thế nào. |
| Giảm chiều của biến | Dimensionality Reduction | Làm nhỏ số lượng biến dưới sự xem xét các biến cơ bản. Theo hocthue.net thì bạn cần phân biệt với phương sai. |
| Định lý giới hạn trung tâm | Central Limit Theorem | Trong lý thuyết xác suất, định lý giới hạn trung tâm phát biểu rằng, trong những điều kiện thích hợp, phân bố của phiên bản chuẩn hóa của giá trị trung bình mẫu sẽ hội tụ về phân bố chuẩn chuẩn hóa. Điều này đúng ngay cả khi bản thân các biến ban đầu không được phân phối chuẩn. |
| Phân phối chuẩn | Normal Distribution | Một phân bố xác suất hình chuông, đối xứng quanh giá trị trung bình |
| Phổ và mẫu | Population and Sample | Tổng thể: toàn bộ các mặt hàng. Mẫu: tập hợp con được thu thập từ một quần thể. |
| Độ lệch | Skewness | Đo lường sự bất đối xứng của phân phối về giá trị trung bình của nó. |
| Phương sai | Variance | Đo độ phân tán của các điểm dữ liệu xung quanh giá trị trung bình của chúng. Theo hocthue.net thì bạn cần phân biệt với hiệp phương sai. |
| Kiểu dữ liệu | Data Types | Các loại dữ liệu như danh nghĩa, thứ tự, khoảng và tỷ lệ. Chi tiết tham khảo tại đây. |
| Xác suất | Probability | Khả năng xảy ra một sự kiện. |
| Xác suất điều kiện | Conditional Probability | Xác suất của một sự kiện dựa trên một sự kiện khác đã xảy ra. |
| Giá trị p và mức ý nghĩa | p Values and Level of Significance | Giá trị p xác định sức mạnh bằng chứng chống lại giả thuyết không. Mức ý nghĩa là tiêu chí để bác bỏ giả thuyết khống. |
| Độ biến thiên | Variability | Mức độ khác biệt giữa các điểm dữ liệu với mức trung bình và với nhau. |
| Lấy mẫu trên và dưới | Over and Under-Sampling | Kỹ thuật phân tích dữ liệu để cân bằng tập dữ liệu (tăng số lượng ở lớp thiểu số hoặc giảm ở lớp đa số). |
| Ước lượng | Estimation | Suy ra giá trị của tham số tổng thể dựa trên mẫu. |
3. Ví dụ cách tính một số khái niệm trong thống kê
Giả sử số lượng người ra vào một quán café được gọi là biến X theo giờ được tính như sau:
| Thời gian | Số lượng người |
| 8 | 1 |
| 9 | 2 |
| 10 | 4 |
| 11 | 4 |
| 12 | 12 |
Chúng ta sắp xếp lại dữ liệu cho nó “khoa học”
| Số lượng người | Số lần xuất hiện |
| 1 | 1 |
| 2 | 1 |
| 4 | 2 |
| 12 | 1 |
Hàm mật độ xác suất của số lượng người như sau:
| Số lần xuất hiện | Xác suất | |
| 1 | 1 | 0,25 |
| 2 | 1 | 0,25 |
| 3 | 2 | 0,5 |
| 12 | 1 | 0,25 |
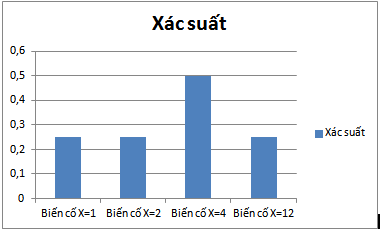
Thông thường nó sẽ có dạng như sau:
- Phương sai và độ lệch chuẩn (variance và standard deviation) là các khái niệm hay đo lường dữ liệu. Chúng ta hãy xét ví dụ về điểm của 1 lớp như sau:
| Điểm | Số lượng học sinh có điểm này |
| 2 | 4 |
| 3 | 5 |
| 4 | 8 |
| 5 | 27 |
| 6 | 12 |
| 7 | 9 |
| 8 | 4 |
Câu hỏi đặt ra là điểm trung bình của lớp bao nhiêu? Nhìn vào dữ liệu trong bảng trên chưa thống kê chúng ta cũng có thể đoán được điểm trung bình trong khoảng 5 điểm.
Trong thống kê, người ta phải đo lường chất lượng mẫu trên bằng các tham số hay chỉ tiêu cụ thể. Người ta sẽ đặt câu hỏi rằng
- Nhiều sinh viên có điểm ở gần điểm trung bình không? Hay là lớp này có 50% học sinh được 2 điểm, 50% còn lại 8 điểm. Bởi vì trung bình cộng cũng khoảng 5 điểm. Hay lớp này 50% đạt 4 điểm, 50% còn lại đạt 6 điểm – trung bình cộng cũng khoảng 5 điểm.
- Dữ liệu trên ta có thể đi tới các khái niệm về hiệp đồng phương sai(Covariance, nói về phương sai giữa các biến ngẫu nhiên), tương quan (Correlation, mức độ mạnh yếu của các quan hệ giữa các biến ngẫu nhiên). Tuy nhiên bạn có thể tham khảo thêm các sách khác.
Ví dụ về
| Điểm | Số lượng học sinh có điểm này | p(x) | X*p(x) | (X-E(X))^2.p(x) |
| 2 | 4 | 0,057971 | 0,115942 | 0,583984 |
| 3 | 5 | 0,0724638 | 0,217391 | 0,342456371 |
| 4 | 8 | 0,115942 | 0,463768 | 0,159776444 |
| 5 | 27 | 0,3913043 | 1,956522 | 0,011835292 |
| 6 | 12 | 0,173913 | 1,043478 | 0,11868168 |
| 7 | 9 | 0,1304348 | 0,913043 | 0,434946988 |
| 8 | 4 | 0,057971 | 0,463768 | 0,463001014 |
| Tổng | 69 | 1 | 5,173913 | 2,11468179 |
E(X)=5,174
Vậy phương sai =2,1146 và độ lệch chuẩn sd=1,45
Ý nghĩa rằng, từ độ lệch chuẩn ta thấy điểm trung bình là 5,174. Độ lệch chuẩn 1,45 ở mức trung bình, chứng tỏ mức độ giao động quanh điểm trung bình của sinh viên toàn lớp (E(X)=5,17) cũng ở mức trung bình. Điều này chứng tỏ cái lớp này tỷ lệ học sinh chênh lệch nhau cũng không nhiều. Điểm của lớp tập chung chủ yếu từ 3 điểm(5,17 -1,45) đến 7 điểm (5,17+1,45).
Kết luận:
Mặc dù có nhiều khái niệm quan trọng về xác suất mà bạn cần lưu ý trong quá trình làm bài tập, làm tiểu luận thống kê phải dùng khá nhiều và đặc biệt là làm luận văn tiếng Anh trong giáo dục sử dụng rất nhiều thống kê. Hocthue.net chúc các bạn hiểu rõ thống kê để làm bài tập, làm luận văn tốt nhất.
Tham khảo:
https://www.hocthue.net/sach-giao-trinh-bai-tap-xac-suat-thong-ke
