1. Giới thiệu về Stata
Stata là phần mềm thống kê mạnh mẽ với các phương tiện quản lý dữ liệu thông minh. Mục đích có thể sử dụng làm nghiên cứu trong quá trình làm luận văn, học các khoá học về định lượng và làm bài tập hoặc làm tiểu luận. Trong hướng dẫn này, hocthue.net sẽ bắt đầu với phần giới thiệu nhanh và tổng quan, sau đó giới thiệu 1 bài tập mẫu và bài giải về stata để bạn hiểu rõ hơn.
Giao diện của Stata cơ bản như sau:
Ở bên trái có cửa sổ có tên "Command" là nơi bạn nhập lệnh cho Stata.
Ở giữa có cửa sổ Stata hiển thị kết quả trong cửa sổ lớn nhất được gọi là của sổ Kết quả.
Ở bên phải có cửa số Biến(variables) liệt kê các biến trong tập dữ liệu của bạn. Cửa sổ Thuộc tính (Properties) ở bên dưới hiển thị các thuộc tính của các biến và tập dữ liệu của bạn.
2. Một số bài tập về stata

Bài giải tham khảo
Câu 1: Giả sử nghiên cứu tỷ lệ tội phạm tại Việt Nam thì mô về phạm tội có thể nghiên cứu bằng các yếu tố ảnh hưởng như sau:
Theo các nhà tội phạm học đã xác định được nhiều yếu tố ảnh hưởng đến tỷ lệ tội phạm như yếu tố xã hội, kinh tế, cá nhân. Một số yếu tố quan trọng nhất được xác định bao gồm:
- Tuổi: Theo các nhà tội phạm học, người cao niên không phạm tội nhiều so với thanh thiếu niên. Họ (các nhà tội phạm học) do đó cho rằng dân số thiếu niên có tỷ lệ tội phạm rất cao.
- Nên kinh tê: Một số nhà tội phạm tin rằng một nền kinh tế nghèo nàn, GDP thấp là nguyên nhân gây ra tỷ lệ thất nghiệp cao và do đó gây ra tội phạm.
- Vấn đề xã hội: Khi mức độ của các vấn đề xã hội tăng lên như số lượng các gia đình cha mẹ độc thân, học sinh bỏ học có thể gây ảnh hưởng đến tâm lý tội phạm.
Mô hình có thể là:
![]()
Câu 2:
a) Đồ thị trung tung FE tức là chi tiêu thức ăn và trục tung TE là tổng chi tiêu như bên dưới.

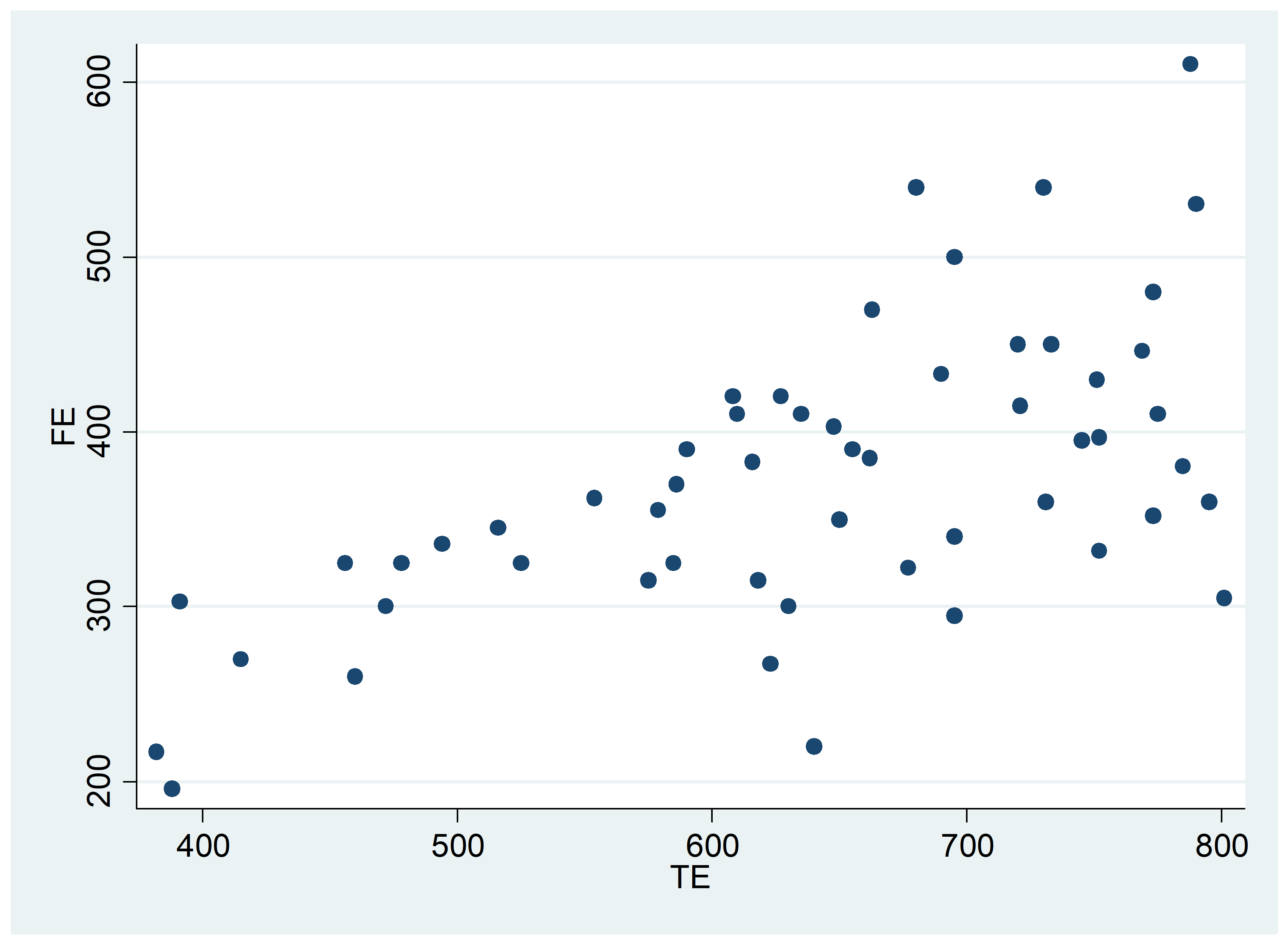
Gọi FE (food Expenditure) là biến phụ thuộc và TE (Total Expenditure) là biến độc lập ta được kết quả mô hình như sau:
|
Source |
SS df |
MS |
Number of obs = |
55 |
|
F( 1, 53) |
= 31.10 |
|||
|
Model |
139022.82 |
1 139022.82 |
Prob > F |
= 0.0000 |
|
Residual |
236893.616 |
53 4469.69087 |
R-squared |
= 0.3698 |
|
Adj R-squared |
= 0.3579 |
|||
|
Total |
375916.436 |
54 6961.41549 |
Root MSE |
= 66.856 |
|
fe |
Coef. |
Std. Err. t |
P>t [95% Conf. |
Interval] |
|
te |
.4368088 |
.0783226 5.58 |
0.000 .2797135 |
.593904 |
|
_cons |
94.20878 |
50.85635 1.85 |
0.070 -7.796134 |
196.2137 |
Ta được mô hình hồi quy tổng thể đó là
FE= 94.20878+ 0.436809FE +u
Do hệ số TE dương nên ta kết luận rằng chi tiêu mua lương thực tăng tuyến tính với tổng chi tiêu.
Câu 3:
a)
Kết qua mô hình giữa ln(wage) và educ như sau:
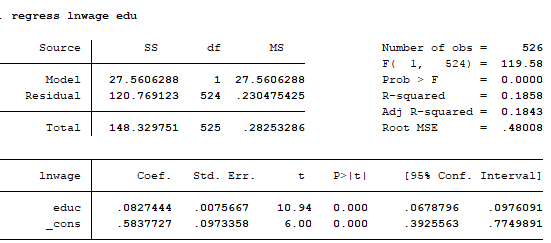

Ta thấy hệ số phù hợp R-squared là 0.1858 ta thấy ý nghĩa rằng giáo dục giải thích 22% của biến lnwage
Hệ số p-value =0 chứng tỏ nếu kiểm định R2 ≠0 . Thông thường nếu p-value =0 có thể kết luận mô hình là có ý nghĩa quan hệ giữa ln(wage) và edu tức là giáo dục có mối quan hệ với logarit tiền lương.
Ta có thể viết lại mô hình hồi quy như sau:
Ln(wage)= 0.5837727 + 0.082744 educ +u
b)
Ta có mô hình như sau:
wage= -0.9048516 + 0.5413593*educ +u
Ta được kết quả và đồ thị sau:
Trong đó hệ đường cao hơn là đường wage và thấp hơn là ln(wage). Ta thấy hệ số thấp hơn bởi vì mô hình hổi quy ln trong một mô hình hồi quy là một cách rất phổ biến để xử lý các tình huống mà một mối quan hệ phi tuyến tồn tại giữa các biến độc lập và phụ thuộc. Sử dụng logarit để đánh giá cho mối quan hệ hiệu quả phi tuyến tính.. Do đó hệ số góc của mô hình ln sẽ thấp hơn mô hình tuyến tính không phải logarit.
Câu 4.
/* Thiết lập 100 quan sát */
set obs =100
/* Thiết lập x từ 1 đến 100 */
gen x=_n
/* tạo u với hàm phân phối chuẩn có độ lệch tiêu chuẩn là 9 và trung bình là 0 */
gen u= rnormal(0,9)
/* tạo y */
gen y= 25+ 0.5*x+u
regress y x
/*Sau đó lặp lại để xem sự thay đổi */
. replace u=rnormal(0,9)
(100 real changes made)
. replace y=25+0.5*x+u
(100 real changes made)
. regress y x

Bảng 50 biến hệ số và hằng số của mô hình bên dưới:
|
STT |
Hệ số |
Hằng số |
|
1 |
0.559146 |
22.01877 |
|
2 |
0.496917 |
24.47293 |
|
3 |
0.559421 |
23.08086 |
|
4 |
0.477793 |
25.17664 |
|
5 |
0.634216 |
24.43563 |
|
6 |
0.531187 |
23.03467 |
|
7 |
0.579003 |
25.34174 |
|
8 |
0.434642 |
24.59241 |
|
9 |
0.425048 |
23.10669 |
|
10 |
0.655447 |
25.23225 |
|
11 |
0.545225 |
24.72915 |
|
12 |
0.440208 |
23.00782 |
|
13 |
0.462175 |
25.05967 |
|
14 |
0.534416 |
24.75997 |
|
15 |
0.486741 |
23.10199 |
|
16 |
0.583187 |
25.22057 |
|
17 |
0.503988 |
24.88844 |
|
18 |
0.407302 |
22.9527 |
|
19 |
0.701233 |
25.26039 |
|
20 |
0.528918 |
24.92657 |
|
21 |
0.428679 |
22.97768 |
|
22 |
0.775209 |
25.26597 |
|
23 |
0.680537 |
25.00867 |
|
24 |
0.499697 |
22.91682 |
|
25 |
0.579524 |
25.30272 |
|
26 |
0.505199 |
25.14032 |
|
27 |
0.437763 |
22.79972 |
|
28 |
0.458293 |
25.18758 |
|
29 |
0.510882 |
25.21255 |
|
30 |
0.412656 |
22.6339 |
|
31 |
0.415013 |
25.35426 |
|
32 |
0.655899 |
25.30749 |
|
33 |
0.437684 |
22.78882 |
|
34 |
0.401382 |
25.34872 |
|
35 |
0.656958 |
25.31893 |
|
36 |
0.419503 |
22.88048 |
|
37 |
0.426417 |
25.42346 |
|
38 |
0.425212 |
25.30239 |
|
39 |
0.401355 |
22.73032 |
|
40 |
0.484928 |
25.43568 |
|
41 |
0.436463 |
25.40308 |
|
42 |
0.412919 |
22.8271 |
|
43 |
0.414379 |
25.30417 |
|
44 |
0.499664 |
25.22376 |
|
45 |
0.401093 |
22.83304 |
|
46 |
0.440595 |
25.42079 |
|
47 |
0.445569 |
25.30174 |
|
48 |
0.440272 |
22.91587 |
|
49 |
0.488007 |
25.24615 |
|
50 |
0.472239 |
25.20093 |
Câu 5:
Trị số P, dù cực kì thông dụng trong nghiên cứu khoa học, không phải là một phán xét cuối cùng của một công trình nghiên cứu hay một giả thuyết.
Thông thường khi nhà khoa học muốn kiểm tra xem liệu phụ gia thực phẩm có gây ung thư hay thuốc chữa bệnh, nhà khoa học cho rằng nó không - giả thuyết không - và sau đó thực hiện thử nghiệm so sánh thuốc hoặc thuốc với giả dược hoặc một loại thuốc khá. Nếu có nhiều người sống sót hơn với thuốc so với giả dược, thì nhà khoa học sẽ kết luận thuốc sẽ hoạt động tốt. Điều này cũng có thể xảy ra để thấy rằng các kết quả này cũng có thể mang tính may mắn.
Trị số P có nhiều vấn đề, và việc phụ thuộc vào nó trong quá khứ (cũng như hiện nay) đã bị rất nhiều người phê phán gay gắt. Cái khiếm khuyết số 1 của trị số P là nó thiếu tính logic.
Thật vậy, nếu chúng ta chịu khó xem xét lại ví dụ trên, chúng ta có thể khái quát tiến trình của một nghiên cứu khoa học (dựa vào trị số P) như sau:
• Đề ra một giả thuyết chính (H)
• Từ giả thuyết chính, đề ra một giả thuyết đảo (Ho)
• Tiến hành thu thập dữ kiện (D)
• Phân tích dữ kiện: tính toán xác suất D xảy ra nếu Ho là sự thật. Nói theo ngôn ngữ toán xác suất, bước này xác định P(D | Ho).
Vì thế, con số P có nghĩa là xác suất của dữ kiện D xảy ra nếu (nhấn mạnh: “nếu”) giả thuyết đảo Ho là sự thật. Như vậy, con số P không trực tiếp cho chúng ta một ý niệm gì về sự thật của giả thuyết chính H; nó chỉ gián tiếp cung cấp bằng chứng để chúng ta chấp nhận giả thuyết chính và bác bỏ giả thuyết đảo
Tài liệu cơ bản về Stata bao gồm Help của Stata và Hướng dẫn tham khảo cơ sở ( Base Reference Manual) về từng mục lớn của Stata từ Quản lý dữ liệu, Đồ họa và Chức năng... Các bạn có thể tham khảo các sách như
Acock - A Gentle Introduction to Stata
Lawrence Hamilton- Statistics with Stata
Scott Long and Jeremy Freese- Regression Models for Categorical Dependent Variables Using Stata (3rd edition);
